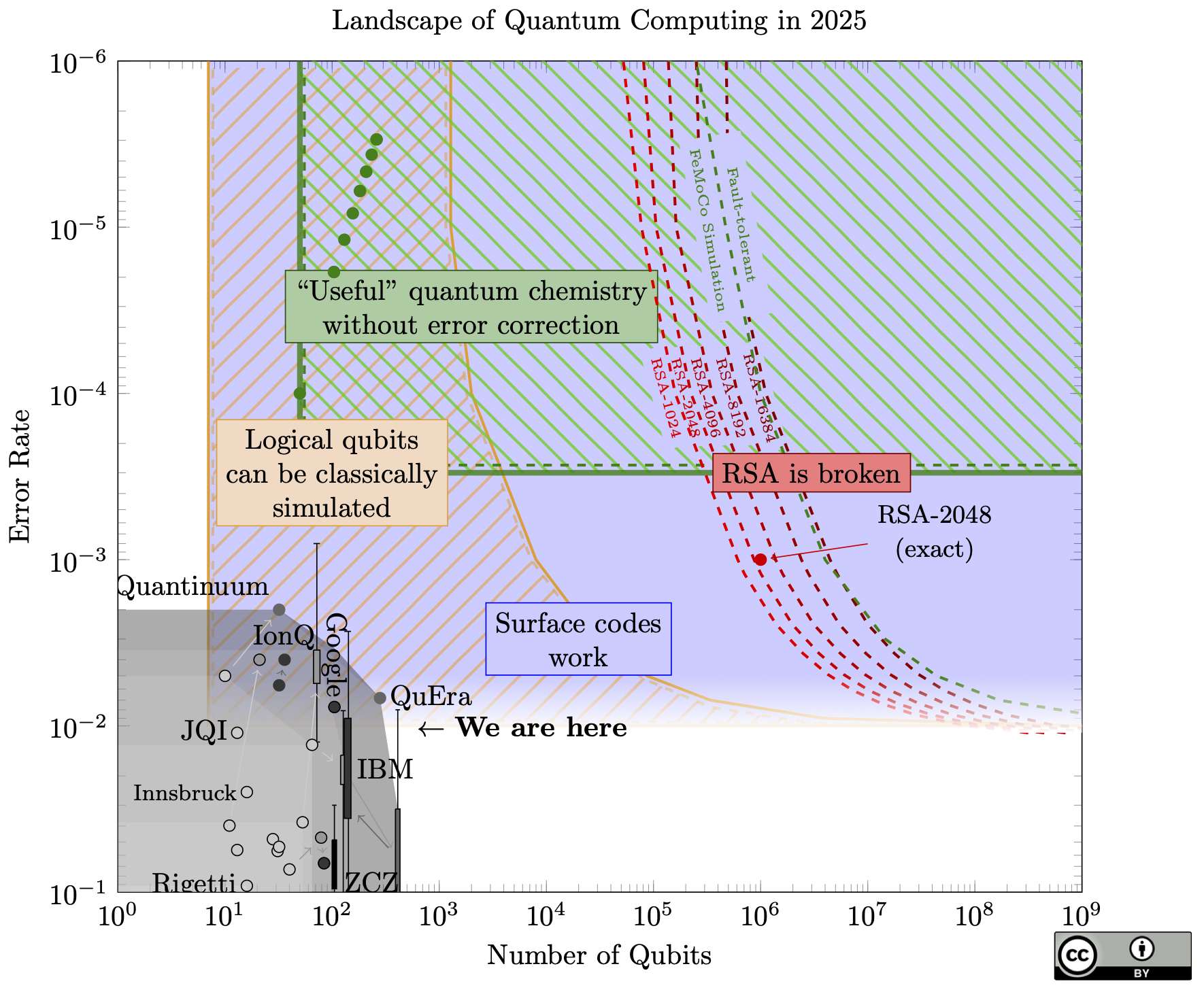
Landscape of Quantum Computing
The big news: the curves on the right (the resources needed to break RSA) have moved by a factor of 20, meaning we only need one million physical qubits to break RSA-2048, thanks to a new paper of Craig Gidney.
To put this in perspective, this brings a quantum attack as much closer to reality as if someone built a 2,100 qubit device this year, and probably more (since we can now avoid any unforeseen scaling difficulties between 1 million qubits and 20 million qubits).
How did this happen? Roughly, 5 years of different improvements in quantum codes and algorithms, all put together. Some of the techniques are the quantum equivalent of "bare metal" coding, and do things like combine codes of different distances and nesting codes together. For this reason it's now much harder to extrapolate the costs at different error rates: large parts of the estimates in the new paper come from expensive simulations. When I reached out to Craig to ask if it could be extrapolated, he said "I would be wary of a simple extrapolation [...] There's probably a simple rule but I wouldn't trust it until simulations confirmed it." I ignored this advice and invented a simple rule just to make a nice chart; it's described in the methodology section below. The red dot is the single exact estimation from Craig's paper.
Unlike some other papers in the past which claimed qubit counts around 1 million or lower, this paper makes no new architectural assumptions: it still assumes just a grid of identical qubits, each connected to only its neighbours in the grid.
If we're imagining an exponential growth in quantum resources (which we haven't seen yet, but we need to if we expect to ever reach 1 million physical qubits), this shaves off 4.3 doublings. Today's physical devices are "only" a factor of 9,500 away (13.2 doublings) from this new target.
A pattern I've noticed lately is that people are cautious about quantum attacks, and so they shrink this gap slightly when they estimate how soon quantum computers will break cryptography. This is a good idea! But it creates a game of telephone: Organization A will be cautious and shave off a year or two in their estimate, then Organization B will take A's estimate and conservatively shave off another year or two, and so forth, until finally someone expects RSA to break later this week. So I want to be clear one million qubits is based on the best known estimate, and this is 9,500 times larger than best known device. It's up to you to add your own margin of caution.
Future improvements?
I had previously (wrongly) said that I didn't expect the red lines to move much. So a spooky question remains: am I still wrong, and the target qubit counts might decrease even further? Consider this chart I recreated from the new paper (Fig. 1), but where I've added a suggestive trendline:
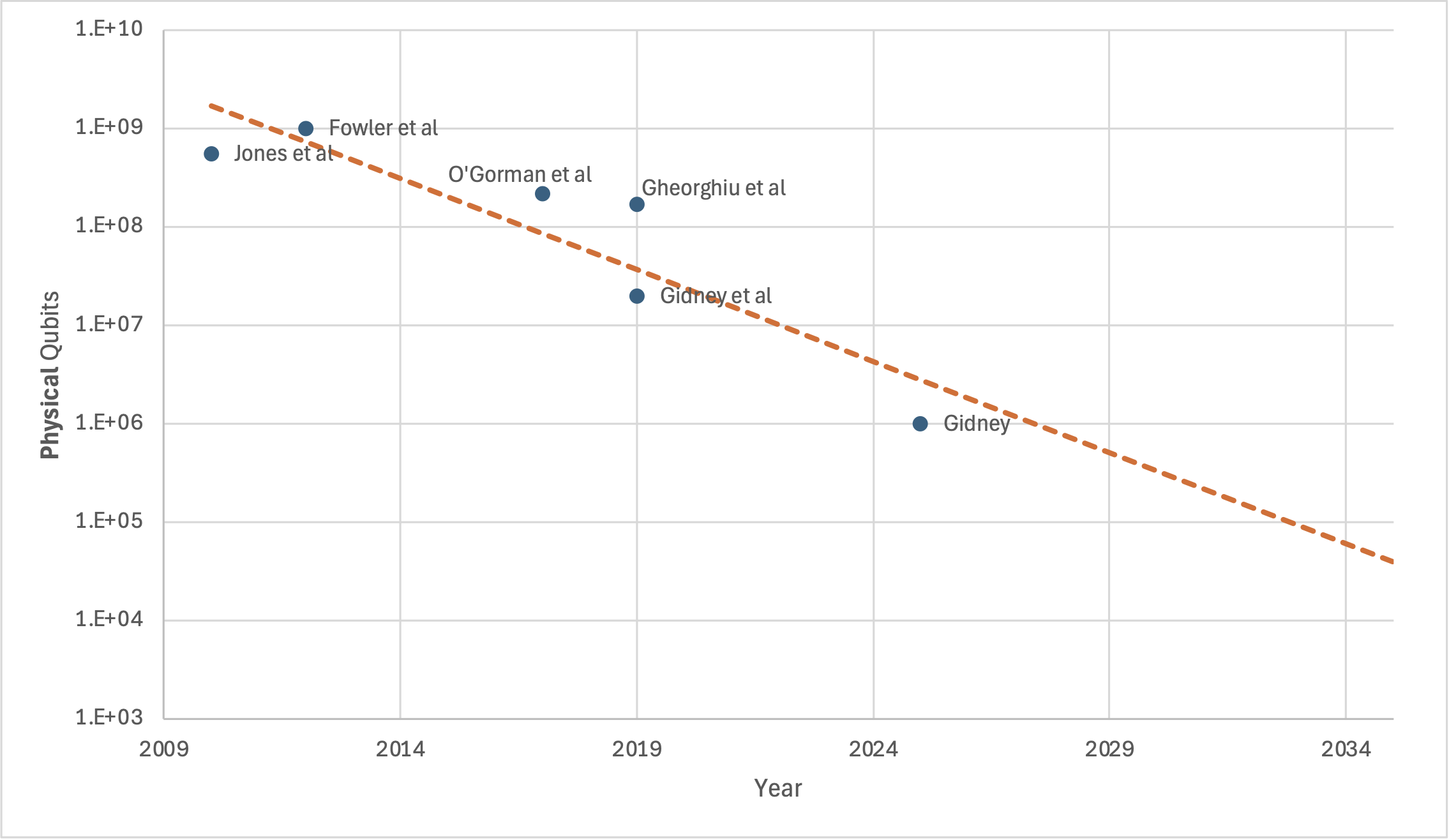
Should we expect to need only 39,000 physical qubits by 2035?
I still don't think it will go down that far. I would be quite surprised if it went down to 100,000 (this would need some seriously insightful results), and I would be truly shocked if it went further. My (somewhat technical) reasoning is below, but Craig makes a good point at the end of his paper about how to interpret this kind of skepticism: "I prefer security to not be contingent on progress being slow".
For a minimum number of physical qubits: there is some minimum number of logical qubits we will need; there is some minimum number of operations we will need; and codes outperforming the surface code seem fundamentally impractical.
On the first point, at some point the number of logical qubits would become so low that we can classically simulate the entire thing. If classical factoring remains hard, we should expect a minimum number of qubits to ensure we have enough "quantumness". Above that, my own hunch is that half the size of the RSA modulus is probably optimal: that's the bit-length of the prime factors themselves, so it should be harder to get enough information to recover them without more qubits (the new algorithm uses roughly half the modulus size already). So I expect at least 1024 logical qubits to factor RSA-2048.
For the operation count, the new algorithms continue to need to do something like modular exponentiation. Again, this feels inescapable without a radical breakthrough: the core quantum technique is to detect a multiplicative subgroup, so you need to do repeated multiplications. If I generously assume we can find a quadratic-time algorithm, we need at least 4 million operations; if these parallelize perfectly, we need a surface code distance of at least 10 (or 242 physical qubits for each logical qubit).
This already puts us at 242,000 qubits, ignoring any extra space for routing or performing operations. To shrink further we would need to improve on the code itself.
I remain skeptical of higher-performance quantum codes, since they require long-range connections between physical qubits that current architectures have not demonstrated at scale. A more promising route is to build on the idea of having some logical qubits in much smaller surface codes, which are themselves encoded in another quantum code, and this larger code can start to forget these locality concerns because it operates on logical qubits. This is one of the techniques this new paper uses, and such techniques will probably improve.
But, even a distance-7 surface code creates a 100:1 physical:logical qubit overhead. In the most extreme version, we would have only one high-distance logical qubit, and the rest in this kind of "cold storage" with distance-7 codes, but this would still need 100,000 physical qubits.
Request
I'm getting uncomfortable with the ratio of attention this chart gets versus how well I can keep up with quantum hardware news (and especially quantum chemistry news). If you keep up-to-date with either of these areas and you want to help out (more or less, point me to the right papers once a year), please reach out through email or social media!
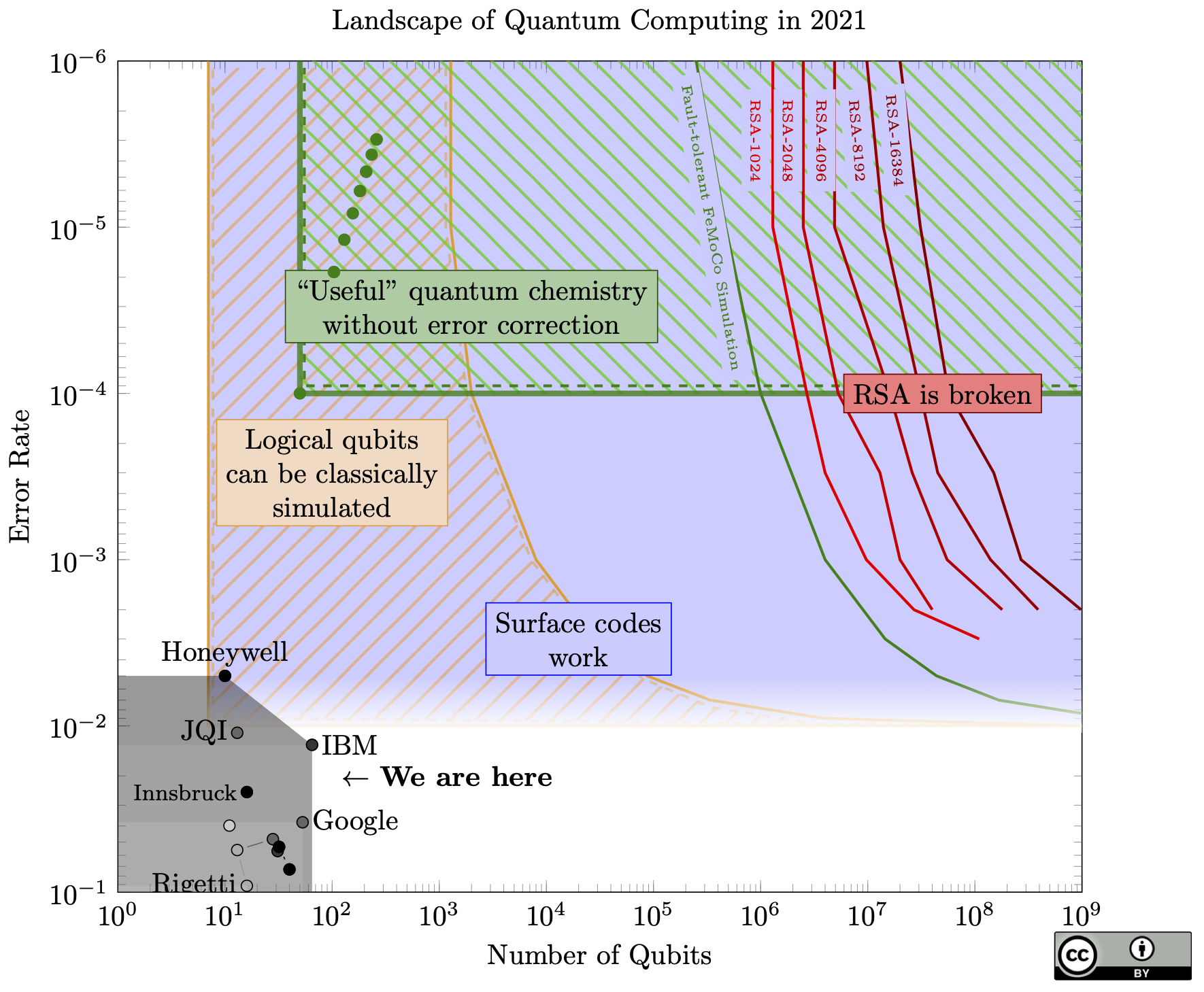
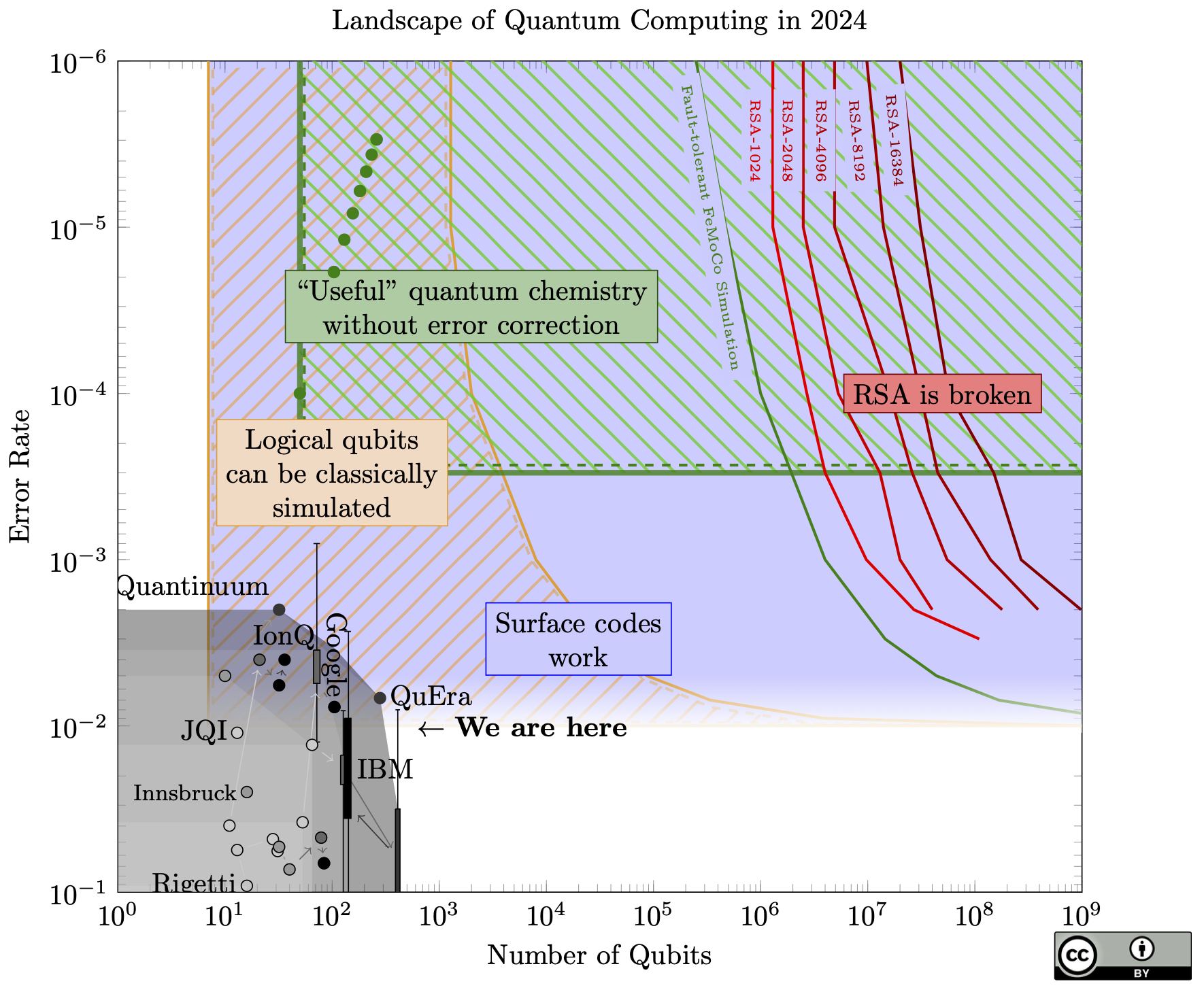
The chart itself shows little change from last year. For example, IBM's chips seem to have moved backwards (fewer qubits, but better fidelity). But this just shows that error rate and qubit count do not capture the full state of quantum computing, since Google's new dot (hardly visible in this chart) represents a huge result: Google created the first logical qubit in the surface code!
A few specific achievements:
- It's beyond threshold, meaning that when they increased the number of physical qubits used to make the logical qubit, the logical qubit had fewer errors
- When they used all the physical qubits they could, the logical qubit performed better than any single physical qubit
- They kept this up for about a million rounds of error correction (roughly 1 second), and decoded the error data in real-time
- Each surface code cycle was roughly 1 microsecond, the same speed as estimated for factoring RSA-2048 in 8 hours
When I first read these results, I felt chills of "Oh wow, quantum computing is actually real".
How does this fit into the path to breaking cryptography? Despite my enthusiasm, this is more or less where we should expect to be, and maybe a bit late. All of the big breakthroughs they demonstrated are steps we needed to take to even hope to reach the 20 million qubit machine that could break RSA. There are no unexpected breakthroughs. Think of it like the increases in transistor density of classical chips each year: an impressive feat, but ultimately business-as-usual.
In fact, they note that their machine suffers correlated errors roughly once per hour. Correlated errors generally break quantum error correction, so that means that even if they made this same machine 200,000x bigger, it still couldn't break RSA.
Another limitation might be the classical co-processor doing the decoding. I can't find the specs on this, but if they need a big classical machine to keep up with the decoding, that's going to cause problems if they try to scale up the runtime and size of the quantum computer.
What's next? I still think that logical qubits will be basically useless until we have at least 40 (and probably many more). However, it remains to be seen whether bigger, better quantum computers can do something useful without error correction in the next few years.
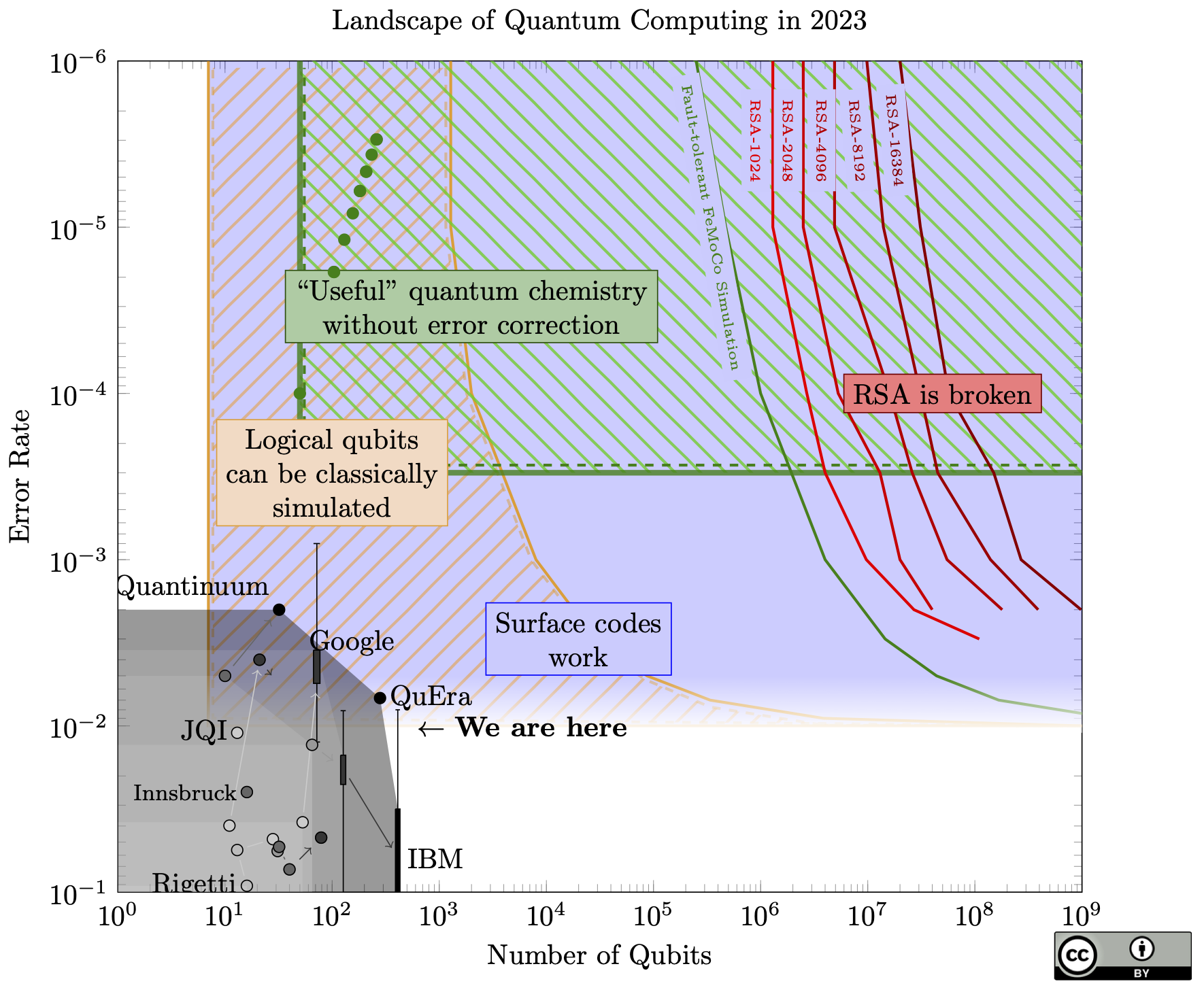
2023 had two big advances in quantum computing that are relevant to this chart.
Firstly, a new quantum factoring algorithm! The new algorithm needs asymptotically fewer gates, but it is unclear right now if that translates into fewer resources in practice. It is a big task to create a complete, optimized circuit that accounts for all necessary error correction overheads, so no one has finished that yet. The proposed improvement is proportional to the square root of the bitlength, so it might be approximately a 45x improvement for an attack against RSA-2048. However, saving 45x in number of operations will not save 45x in qubits, so the red lines on the chart may not move that much.
Still, I said in 2021, "An asymptotic improvement is highly unlikely". Whoops!
The biggest experimental news came out just before the end of the year, with a collection of impressive error correction results. Like Google's result last year, this group (from QuERA, Harvard, JQI, and MIT) show that the logical qubits improve as the code gets larger, but the new result goes up to distance 7 (for context, error correction in Shor's algorithm would need distance around 25-30). They were also able to perform an operation between two logical qubits.
Other results from that paper use a colour code. Colour codes share many of the good properties of surface codes (they fit on a flat chip and suppress errors well), and either type of code could lead us to breaking RSA.
They also perform a number of algorithms on logical qubits with smaller codes. These results are less relevant to this chart and breaking RSA, as the smaller codes do not have the scaling guarantees that a surface code does.
While Google and IBM use superconducting qubits, this group used neutral atoms. It was harder to find a specific number for fidelity from their paper, so take the dot on the chart with a grain of salt (as in previous years, compressing qubit quality to a single dot is imprecise and loses a lot of information). For more discussion on this result, see Scott Aaronson's blog (note especially Craig Gidney's critique in the comments that they do not do multiple rounds of error correction, something that is absolutely necessary for quantum computation at large scales).
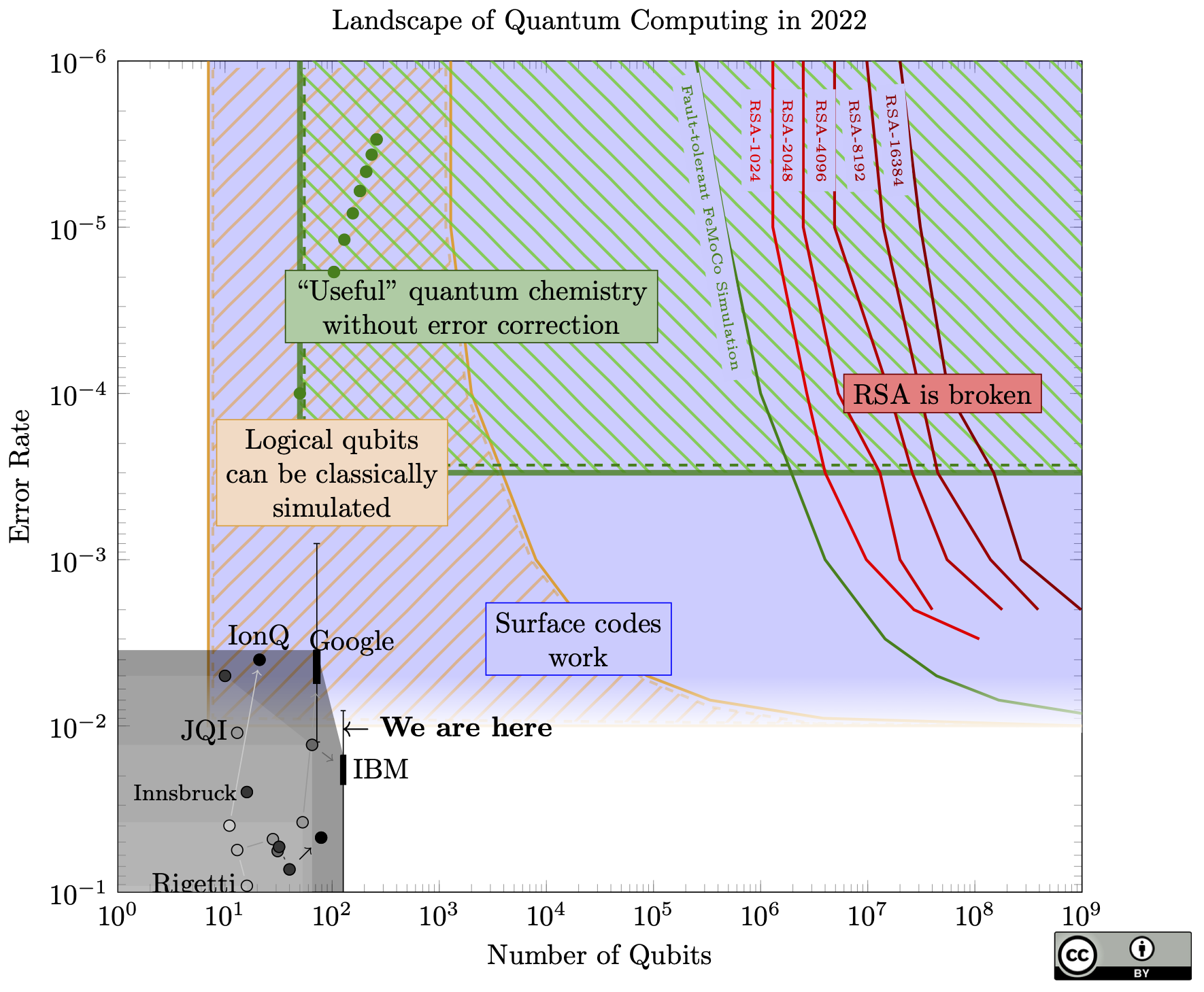
The key differences this year:
- Google implemented a surface code on their "Sycamore" chip, which they also expanded to 72 qubits. Like the results from other groups last year, the logical qubit is worse than the physical qubits, but the exciting fact is that when they use more physical qubits, the logical qubit gets better. This means if they had enough qubits, they should be able to make a logical qubit that works better than the physical qubits.
- The other big news: IBM released data from its 127-qubit Eagle processor. I have a cynical hypothesis: it wasn't quite ready to demonstrate when they announced it last year, but they had to make an announcement since they had just made their quantum roadmap in 2020, and it would look really bad to fall behind only one year after making the plan. I'm still impressed, even if it's slightly late. They have also announced a new 433-qubit chip, which I have again excluded from the chart because there is no data on qubit quality yet.
- I plotted both IBM and Google's latest results in a box-and-whisker, to show the variance in quality of individual qubits.
- The "Useful quantum chemistry without error correction" moved down, based on the conclusions in this paper. The improvement is "error mitigation", a collection of techniques that are simpler than full error correction, but offer fewer guarantees. I still can't claim that the chemistry will actually be "useful" (I don't think the paper does either), just that it might answer a real chemistry problem that classical computers can't.
If you compare this to last year's chart it seems like there were big breakthroughs in qubit quality. I'm not sure, since my methods of producing a single number for "qubit error" weren't rigorous. There seems to be progress, but I wouldn't claim any precise trends.
Other news that doesn't fit on the chart:
- There's been some work on error correction where the logical qubit actually lasts longer than the physical qubits (e.g. here and here), but I'm not sure the error correction they used will scale very well .
- There were huge breakthroughs in quantum "LDPC" codes, which promise much better performance than surface codes. The catch: they need arbitrary long interactions between qubits. In contrast, the surface code can use qubits that only interact with their neighbours in a grid (Google and IBM's qubits are on a grid, Honeywell's qubits are not). For this reason I'm not optimistic about LDPC codes, but other people are.
Besides those, not much has changed. The main conclusions from last year still hold:
- We need exponential improvement to get anywhere.
- There is a big dead zone where quantum computers might be completely useless.
- Switching to quantum-safe cryptography today is still a good idea (this year NIST announced which quantum-safe cryptography it will standardize).
Quantum computers have a lot of potential, but how far are we from that potential? When will all of our RSA keys be obsolete? When will -- as Microsoft hopes – quantum computers solve climate change?
I drew a quick sketch of my impressions of the field on Twitter, and Steve Weis asked for a more detailed treatment. Here is a more accurate picture of that sketch:
(Undoubtedly this chart is still incomplete. If you think some of the points on this chart should move, please send me a message and ideally a citation!)
Some terminology: A qubit is the basic unit of data in a quantum computer, and it can store a 1 or a 0 just like a classical bit, but also superpositions of those two states. A gate is an operation applied to a qubit, such as flipping a 0 to a 1, or changing the quantum phase, or XOR, etc.
To explain this chart: quantum data is very fragile. Most types of qubits today can only hold onto a quantum state for a few microseconds before they lose it – either they drift to another quantum state unpredictably, or they interact with the environment and "collapse" any superposition they had.
Not only that, any gate applied to the qubit has some chance of causing error. Today’s qubits are close to 1% gate error. Imagine if every time you sent a bit through a transistor, there was a 1% chance of flipping the bit. You could hardly perform any computation at all!
Google’s Sycamore chip, famous because it seems to be able to solve a (useless) computational problem faster than any classical computer, can only do about 20 gates in a row before being reduced to useless noise. To break RSA-2048 would require more than 2.1 billion gates in a row.
For quantum computers to be useful, we need more qubits but we also need better qubits.
Rather than make each qubit a billion times better, the agreed-upon approach is to make them about 10-100 times better, then assemble these qubits together with an error-correcting code. The individual qubits on the chip are known as physical qubits, and connecting together 100s or 1000s of physical qubits can give one logical qubit. Without improving the quality of the individual physical qubits, the error rate of the logical qubits can be reduced exponentially just by bundling more physical qubits into each one. The only catch: the physical qubit error rate must be lower than a certain threshold before the code will function at all.
A quantum computer that uses error correction to push qubit and gate errors to 0 is called fault-tolerant.
The front-runner for a quantum error-correcting code is called a surface code. The blue region in the chart is where physical qubits are good enough to form logical qubits in a surface code. After some feedback, I added a fade to the bottom of that region, since we're not exactly sure what the threshold is (very likely between 0.1% to 1%, but it depends on what kind of errors happen).
We’re very close to this! However: If we need 100 physical qubits to make a single logical qubit, then that increases our qubit requirements by a factor of 100. And 100 is an underestimate: longer algorithm’s like Shor’s algorithm (to break RSA) likely require more than 1000 physical qubits per logical qubit.
There has been some talk about quantum computers reaching a point where they cannot be simulated classically. Quantum computers have already passed this point, since classical computers can only simulate about 40 qubits (each qubit doubles the time or memory complexity of the simulation, so even huge classical computers can’t go much higher than this).
However, once we start bundling physical qubits into logical qubits, then the number of qubits which are actually useful (the logical qubits) is much lower than the number of physical qubits. Even if we have 40,000 physical qubits, if we only get 40 logical qubits once we bundle them together for error correction, then any algorithm on those logical qubits is still within reach of classical computers.
The yellow-///-striped region of the chart is where we can’t simulate all the physical qubits, but there are so few logical (error-corrected) qubits that we can classically simulate any error-corrected algorithm.
The bottom left region is bad for quantum computers: if the gate error is 10-3, we can only run about 1000 gates on the physical qubits, probably not enough to do anything useful. But we can’t make enough logical qubits to do anything useful, either!
Once we have decent error rates (say, 10-3) then we just need to build lots of qubits and we can start doing useful things. However, the number of qubits for these fault-tolerant algorithms can be very high.
The green line shows the minimum requirements for a chemical simulation of FeMoCo, a molecule involved in producing ammonia from atmospheric nitrogen.
The red lines show the minimum requirements to run Shor’s algorithm to break RSA keys of various sizes.
What about to the left of that green line? If you had 10,000 qubits but 1 in 1000 gates caused an error (i.e., 100x more qubits and 10x less error than today), could you still do something useful? We’re not sure. There are promising approaches, mainly variational quantum algorithms, which can be more robust against noise and can use error reduction techniques with lower overheads but less benefit than full fault-tolerance. The problem with these is that there are few provable guarantees on their effectiveness. They might work really well, or they might not, and maybe we won't even know until we can actually build a quantum machine and try them. There is a lot of research in this area, under the term “NISQ”: Noisy Intermediate Scale Quantum computers.
The green-\\\-striped region shows where we can solve some chemistry problems using quantum computers, without needing full error correction. The green dots are resource counts for some specific problems.
From this chart, here is my opinion on the prospects of quantum computing:
- Outside of the green striped region and to the left of the green line, quantum computers might be useless. This is a region where we cannot run any quantum algorithm which outperforms classical computers. Though, we may discover new algorithms which could run on a quantum computer in this region.
- We need Moore’s-law type scaling for quantum computers to ever be useful. This is a log plot. If we ever want to get to the regions on the top or the right, we need to be scaling exponentially in some dimension.
- There may be a sharp transition from “quantum computers are useless” to “quantum computers break RSA”. If we do get exponential scaling, then the distance we have to cover from here to the green line (the first useful application on this chart) is much farther than the distance from there to where all reasonable RSA sizes are broken.
- The green-striped region will probably move down.
- First, it’s the most outside of my expertise and the most likely for a paper that I don't know about.
- Second, there is a lot of research in this area.
- Third, these are exactly the kind of problems where I would expect the real-world performance of algorithms to vastly exceed the worst-case performance of a theoretical analysis. But we won’t get to see that real-world performance until the big quantum computers are built!
- The red lines probably won't move much. Unlike with variational problems, we can estimate the runtime and success probability of Shor's algorithm with known algorithms very precisely. Moreover, Shor's algorithm is mainly just modular exponentiation, meaning that it's about as hard for a quantum computer to use RSA as it is to break RSA. An asymptotic improvement is highly unlikely, though small algorithmic improvements and better codes will probably develop and shift the curves a bit to the left. Also, variational algorithms won't break RSA.
- A big breakthrough could change this whole chart - but a big breakthrough could also break factoring classically. If someone comes up with a code much better than the surface code, then this all radically changes; if someone beats O(n2/log n) multiplication on a quantum computer, the red lines move. But these would be big innovations; we could also get a polynomial-time classical factoring algorithm. How do we decide which scientific breakthroughs are plausible, and which aren’t?
- Even though quantum computers are far away, you should still replace RSA and ECC. Michele Mosca pointed out the main problem: Suppose quantum computers that can break RSA-2048 are 30 years away. If it will take 10 years to standardize new cryptography, 10 years for your organization to implement it, and you need your secrets to remain safe for 12 years, then you’re already 2 years too late, since someone can record your encrypted data and break it later. Basically, it’s a race between the world’s most brilliant quantum engineers and the world’s laziest sysadmins, where the sysadmins have about a 30 year headstart.
Feedback
I posted this on Twitter and received good feedback, which I partially address here:
- Rodney van Meter says that architecture and clock speed are important to consider as well. Getting to 10 million qubits hides a lot of architectural issues: are we really going to build a stadium-sized chip and a refrigerator to house it? Probably not; instead we'll either switch to a new technology or connect many smaller processors. Either way we may end up needing to change the circuits/algorithms to fit the architecture. The fault-tolerant lines on the chart assume a huge, 2-dimensional grid of qubits, each connected only to its neighbours. I mildly disagree about clock speed: today's gates are about as fast as they need to be run the fault-tolerant algorithms on this chart in a matter of hours to weeks. If we move to a different technology, though, maybe we get lower errors but longer gates, and gate times will be limiting.
- BSI Bund has a similar chart (pg. 208, Fig. 21.1). They plot qubits*depth, which is a more meaningful thing to count, but probably more confusing if you're new to quantum computing.
- This chart might be overoptimistic in a few ways: Some people doubt the threshold theorem altogether (it's proven based on uncorrelated errors, so if that assumption is wrong in practice, the codes won't work as expected), and the usefulness of the "useful" quantum chemistry is debatable. Simulating FeMoCo doesn't necessarily give us any better method to produce nitrogen fertilizer, and even if it did, that doesn't fix the unsustainable farming practices that need so much fertilizer. The other quantum chemistry dots aren't huge open problems in the field, but just real-world problems that are beyond classical computing power.
- Google's chip is closer to the surface code threshold than this chart shows, since I used the readout error and other types of error are much lower. There is a complicated relationship between the threshold and the various types of error that I don't fully understand.
- The reason the yellow region of simulatable logical qubits doesn't extend further down/left is because there are no logical qubits in that region. There's also a region where we can simulate all physical qubits, but adding that would clutter the chart.
- To break elliptic curve cryptography (from 256 to 512 bits), the lines are roughly around the FeMoCo simulation line. There is no analysis of quantum elliptic curve circuits with as much detail as for RSA, so the lines would be less accurate.
- Current chips:I didn’t read any of these papers carefully, I just took the numbers, and I always take the worst number I can find. This is often slightly unfair, but I do this so no one can "cheat" with a device that has some abysmal error type.
-
- Google’s 2019 gate error is based on readout error from this talk. Readout error might be unfair to Google here (especially since I couldn't find it for IBM's chip). I excluded the Bristlecone chip because its performance hasn’t been as impressive, despite higher qubit counts.
- Google 2022 came from here, where I used the CZ error for the box-and-whisker chart. I listed the number of qubits as 72 (the total on the device) even though the paper only uses 49 (so maybe other qubits are much worse or non-functional).
- The 2024 Willow data comes from the table in their blog post.
- Innsbruck was based on a 2.5% error rate in XX-rotations.
- Bottom IBM and Rigetti come from this survey paper; I took the largest type of error in every case.
- Top IBM was from this IBM paper, where I used 1 - fidelity as error.
- Other IBM data points come from their live data. I exclude qubits if their error rates are 1.0.
- For JQI (Joint Quantum Institute) I also used 1 - fidelity, with the mid-point of their fidelity estimate (98.9%).
- For the 2022Honewell point, I used the worst error type (measurement) from their simulation parameters (which are based on experiment and worse than all experimental error types they list in that paper)
- QuEra came from here, where I used the physical qubit initialization fidelity of 99.3%.
- Rigetti's numbers came from here.
- In 2023, Honeywell's dot was merged into the path for Quantinuum, with the latest number here.
- IonQ comes from this page, based on the fidelity of two-qubit gates.
- Rigetti's new numbers came from here.
- IonQ comes from this page, based on the fidelity of two-qubit gates.
-
- Red lines for RSA:
- For before 2025: they came from the python script with this paper. The script crashes if the physical error rate is too close to the threshold, so I took the lowest rate before the program crashed.
- After 2025: the one exact dot is from Gidney 2025, and the dashed lines come from my own Python script, hastily extrapolated from the new paper to other physical error rates. One of the main issues is the yoked surface code. As Craig told me in an email "...there are substantial finite size effects in play due to needing the surface codes to be large enough for the yoke measurements to be pretty reliable.". As a plausible lower bound, I assumed that if the underlying surface code hit the same logical error rate, it should behave the same. Thus, I assumed the same overhead for yoking (a 1.5 factor increase, found by dividing the qubit count of a distance 11 code and the reported qubit counts from the paper), then just found the minimum distance to hit the same logical error rate of a distance 11 code (10-7) when the physical error rate gets smaller, and used that.
To find the logical error rate of a given surface code, I used the same formula as previous years: C * (physical error rate/T)((distance + 1)/2), where C and T are constants, but I took the C and T from Figure 6 in Gidney 2025 by selecting which T would match the scaling of 3.5-d (T=0.1225), and which C would then match 10-15 logical error at d=25 (C=0.14).
- Yellow region is based on a surface code where the error at distance d is given by 0.1*(e/0.01)(d+1)/2, where e is the physical error rate, and requiring error of 10-6 overall (less than that and it’s probably not a very useful algorithm).
- The green line used the same surface code formula to extrapolate the numbers from this paper to different physical error rates.
- The green region is based on this paper, which needs 50 qubits and gate errors less than 10-4, and also this paper. In the second paper I took the number of qubits from Table 4, and assumed the error must be the inverse of (# of qubits)*(circuit depth), where circuit depth was 5*(# of qubits) -3. Since anything above and to the right of any of those dots would also be able to compute the same algorithm, that was where I drew the green region.